Identifying special situations in factoring

• Difference of two squares
• a²- b² = (a + b)(a - b)
• (x + 9)(x − 9)
• (6x − 1)(6x + 1)
• (x³ − 8)(x³ + 8)
• Trinomial perfect squares
  • a² + 2ab + b²= (a + b)(a + b) or (a + b)²
    • 
      
      
    • 
      
  • ^{a2 - 2ab + b2 = (a - b)(a - b) or (a - b)2}
    • 
      
• Difference of two cubes
  • a³ - b³
    • 3 - cube root 'em
    • 2 - square 'em
    • 1 - multiply and change
      • 64x^-1
      • x^3-216
• Sum of two cubes
  • a³ + b³ 
    • 3 - cube root 'em
    • 2 - square 'em
    • 1 - multiply and change
      • x^3+27= (x^3)(x^2-3x+9)
      • 8x^3+27
      • x^3=25
• Binomial expansion
  • (a + b)³ = a^3+3a^2b+3ab^2+b^3
  • (a + b)⁴ = 

End Behaviors/Naming Polynomials

Linear Equations: 

y= mx+b 

1 degree

0 turns 

Domain - x values
Range - y values referred to as f(x)

When M is Positive: 

domain → +∞, range → +∞ (rises on the right)

domain → -∞, range → -∞ (falls on the left)

When M is Negative 

domain → -∞, range → +∞ (rises on the left)

domain → +∞, range → -∞ (falls on the right)

Quadratic Equations (parabolic equation)

y=ax² 

2 degree 

1 turn

(a+b)(c+d)

 

 when A is positive. 

when A is negative.

End Behaviors/Naming Polynomials

Naming Polynomials: 

--Number of turns is always 1 less than the degree. 

Degree:

0- Constant 

1- Linear

2- Quadratic 

3- Cubic

4- Quartic

5- Quintic 

6 to ∞- nth Degree 

Terms:

Monomial 

Binomial 

Trinomial 

Quadrinomial 

Polynomial 

domain → +∞, range → -∞ (falls on the right)

domain → -∞, range → -∞ (falls on the left)

domain → +∞, range → +∞ (rises on the right)

domain → -∞, range → -∞ (falls on the left)

identify quadratic functions

Standardform: ax² + bx + cy² + dy + e= 0

If a=c, then the equation is a circle.If you have an equation like 5x² + 5y²=25 

If a or c, are different signs the equation is a  hyperbola. Like this equation 2x² - 2y²= 6

If  a can NOT = c, and they are the same signs then the equation is an ellipse.  this equation would looke like  4x² + 2y²= 25
If a or c= 0, then  the equation is a parabela. it would look something like this 2x² + 4y= 3.

multipling Matrices

Dimensions statement:
2 X 2 times 2 X 1

These matrices can be multiplied, so you would multiply row X column.
Then you get the sum of the products.
The numbers in yellow tell you that you can multiply the matrices.
The numbers in red tell you the size of the final matrix. 

 

describe graphing

x

 




 Y=a abs(x-h)+k

• When ever you have these types of graphes the general shape will look like a “v” or it will be upside down indicating a negative is in the a part of the equation . 
•  
• You find the vertex by the H and the K in the equation , one key thing to remeber is that the H is always the opposite to the equation . 
•  After finding the vertex them you can graph   

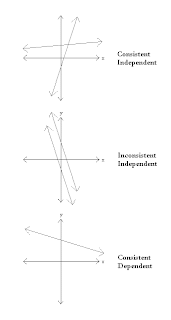
types of systems

 Consistent-Independent. One solution. Lines that have different slopes.

Consistent- Dependent. All numbers/infinite.Lines that have the same slope, and same y-intercepts.

Inconsistent-No solutions and parallel. Lines that have the same slope, but different y-intercepts.